液化石油气(LPG)是石油气经加压或降温后形成的液态烃混合物。LPG的组分, 各地都不一样, 这主要是由原油产地、炼制加工工艺和操作条件的不同所决定的。根据《油气田液化石油气(GB 9052.1-1998) 》标准, 液化石油气是指以丙烷、丁烷为主要成分的液态石油产品, 一般有商品丙烷、商品丁烷和商品丙、丁烷混合物几种。商品丙烷主要是由丙烷和少量的丁烷及微量乙烷组成, 适用于使用时要求高挥发性的产品; 商品丁烷主要由丁烷和少量的丙烷及微量戊烷组成, 适用于使用时要求低挥发性的产品; 商品丙、丁烷混合物主要由丙烷、丁烷及少量的乙烷和戊烷组成, 适用于使用时要求中挥发性的产品。由于LPG组分及含量诸多不同, 在不同温度下饱和蒸气压差别也较大。工程上为了准确地确定LPG的露点必须要估算LPG的饱和蒸气压; 同时, 在LPG储存、运输、使用过程中, 也需要估算LPG的饱和蒸气压是否在储存容器的安全裕度内; 特别是处于池火灾、喷射火、热辐射等火灾环境中的LPG罐, 饱和蒸气压大小的估算对火灾扑救具有重要的意义。

饱和蒸气压可以通过实验测定、理论计算以及经验公式近似计算。早在1801年, Dalton认为:“如果温度按照代数级数的规律增加, 则饱和蒸气压会按照几何级数的规律增加”, 这被认为是文献中所记载的最早的关于p-T关系式之一, 即lgp=a+bT。这是饱和蒸气压理论计算的一个开端。随着对热力学理论认识的深入, 出现了克劳修斯—克拉珀珑方程, 这是所有计算饱和蒸气压经验公式的理论基础。根据此理论以及众多物质的实验数据, 学者们推荐了各类计算饱和蒸气压的方程式和经验公式, 其中, 最简单的公式为wrede-cox方程。最著名且使用最广泛的为Antonio方程。下面是提及到的各类方程^[1]:

由热力学理论导出Clausius-Clapeyron方程:

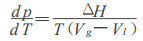(1)

其中:p为饱和蒸气压; T为温度; ΔH为气体的蒸发热; V_g、V_l为气体、液体摩尔体积, V_g>>V_l。

(2)

其中, z为压缩系数; R为气体常数。

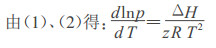(3)

若假定: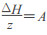, 则

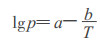(4)

即Wrede-Cox方程。

若假定: 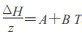, 则

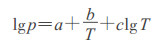(5)

即Rankine方程。

若假定: 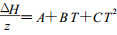, 则

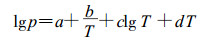(6)

方程(4)的其他衍生方程还有著名的Antoine方程:

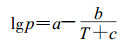(7)

以及增加校正项后的Thomson方程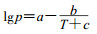+cT等。

饱和蒸气压估算最常用的方程式是(4)和(7), 方程(4)过于简单, 其假定条件气体的蒸发热与压缩系数的比值为常数不是很合理, 因此, 适用范围比较窄。通过对方程(4)进行校正后可得到(5)、(6)、(7)等衍生方程式。笔者认为采用方程(5)和方程(7)估算饱和蒸气压是一种较优的途径。采用方程(5)可以直接通过可信赖的实验数据线性拟合即可得到饱和蒸气压估算公式, 采用方程(7)需要对解析计算出来的常数初值反复优化, 略显复杂。因此, 本文选择方程(5)对LPG饱和蒸气压进行估算。

1 饱和蒸气压估算

根据表 1中数据, 按照方程(5)求解任何温度下LPG饱和蒸气压的大小。具体计算过程如下:①对各组分任意选择三组数据(T, P), 代入方程(5);②建立线性方程组AX=B, 确定向量A_3×3, B_3×1, 求解X_3×1。即为方程(5)中a, b, c的初始解向量X0;③对各组分20组数据变换后赋予温度向量T_20×3、饱和蒸气压向量P_20×1, 则计算P方差初值为:d0 = ||T_20×3·X_3×1- P_20×1||/20;赋予方差允许的误差范围ε初值(10^-6); 4.改变向量X_3×1的各项元素a, b, c的变化范围90%~110%, 选择合适步长做循环; 5.反复求解新的P′_20×1=T_20×3·X′_3×1向量的方差d, 若d < d0, 则d赋给d0, 记下此时的P′_20×1, 向量P′_20×1赋给P″_20×1、方差d赋给d′以及X′_3×1赋给X″_3×1。否则返回上一步继续循环游走搜索, 直到d < ε时或循环结束时退出循环, 此时的d′为最终方差, X″_3×1为最终常数项a, b, c, P″_20×1为最终估算值。

表 1

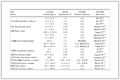
表 1    不同温度(K)下LPG各组分饱和蒸气压(MPa)的数据表[2]

表 1    不同温度(K)下LPG各组分饱和蒸气压(MPa)的数据表[2]

以LPG占比最大的丙烷、丙烯为例, 饱和蒸气压的估算值及相对误差如表 2所示。

表 2

表 2    不同温度下丙烷、丙烯饱和蒸气压(MPa)估算及误差

表 2    不同温度下丙烷、丙烯饱和蒸气压(MPa)估算及误差

当T在258K~353K区间内, LPG各组分饱和蒸气压可用表 3所示的公式估算, 其平均相对误差能够控制在1%范围之内。

表 3

表 3    LPG各组分饱和蒸气压估算公式及误差

表 3    LPG各组分饱和蒸气压估算公式及误差

当T在258K~353K区间内, 由于LPG饱和蒸气压较小, 可以看做理想气体进行估算。由拉乌尔定律可知:P_i=P_si·X_i, 其中, P_i为LPG各组分液化气体的蒸气分压; P_si 为LPG某组分纯液化气体的蒸气压; X_i为某组分纯液化气体的摩尔分数。由道尔顿定律可知:P=ΣP_i, 其中P为LPG的蒸气压。因此, P=ΣP_i=ΣP_si·X_i (8)。

采用表 3所示的饱和蒸气压计算公式及方程(8)利用VB等开发的小软件就可以比较准确地估算各个温度下饱和蒸气压的大小。例如, 若LPG气体的液相分子组分为丙烯27.89%、丙烷26.03%、异丁烯24.16%、异丁烷21.92%, 其15℃~70℃的饱和蒸气压按表 3和公式(8)计算后所绘制的曲线如图 1所示。从图中曲线的斜率变化情况可以看出, 此LPG的饱和蒸气压随温度升高呈现加速增长的态势。例如在0℃~20℃, 温度每升高1℃, 饱和蒸气压平均升高0.13 MPa; 在20℃~40℃, 温度每升高1℃, 饱和蒸气压平均升高0.20 MPa; 在40℃~60℃, 温度每升高1℃, 饱和蒸气压平均升高0.29 MPa。

图 1

图 1     示例组分LPG饱和增气压与温度的关系曲线

2 结语

LPG饱和蒸气压可以通过克劳修斯—克拉珀珑方程推导出的多个衍生方程进行适当的修正求解得到。本文采取了Rankine方程以及已有的实验数据导出了LPG各组分的饱和蒸气压与温度的关系式, 在258K~353K温度区间内, LPG各组分饱和蒸气压平均相对误差都能够控制在1%范围之内, 说明了公式具有较好的适用性。对于不同组分不同含量的LPG可以绘制其饱和蒸气压随温度的变化曲线P=f (T), 通过曲线能够直接读取不同温度饱和蒸气压数值, 从曲线的斜率变化还可以看出, 饱和蒸气压随着温度的升高呈现几何倍数的增加。

参考文献

[1]	卡拉佩奇扬茨МХ, 程光钺. 碳氢化合物的沸点和饱和蒸气压[M]. 北京: 科学出版社, 1963: 38-60.
[2]	《煤气设计手册》编写组. 煤气设计手册(上)[M]. 北京: 中国建筑工业出版社, 1983: 28-33.
[3]	于碧涌, 焦文玲, 等. 液化石油气露点计算的程序设计[J]. 煤气与热力, 2005, 6.