RGM是计算天然气组成及其发热量的基础，通过比较未知样品和已知不确定度RGM的响应值就可以测定样品中各组分的含量。如果RGM所标示的含量有误差，同样也会给样品分析结果带来分析偏差。不管分析偏差是否存在，RGM中各个组分的不确定度都会影响由其导出的(分析)结果的不确定度。
RGM的证书上应列出其经认证的组成，其中每一个组分应皆可溯源至国家或国际标准，并标示出其不确定度。在证书声明的有效期限内，这些数据应是稳定的，可通过标准规定的制备方法或与国家计量实验室颁发的基准参比气体(PRM)混合物比较来获得组成数据。目前，在我国此类RGM应按国家标准GB/T 5274《气体分析-校准用混合气体的制备-称量法》的规定制备，并按国家标准GB/T 10628《气体分析-校准用混合气体组成的测定和校验-比较法》的规定确定其中各组分含量。表 4所示为天然气研究院进口的、由英国国家物理实验室(NPL)以称量法制备的一种适用于能量计量系统的RGM。表 4中数据表明，RGM中的组分数为10个，浓度最高的CH4组分的测量不确定度达到0.02%的水平[1]。
EffecTech公司是通过英国皇家认可委员会(UKAS)认可的检测和校准实验室，并可按国家标准GB/T 15481(IDT ISO 17025)《检测和校准实验室能力的通用要求》规定的范围提供具有规定不确定度数据的RGM[5]。RGM由称量法制备，制备的RGM经充分混合后，与由英国国家物理实验室(NPL)或荷兰国家计量研究院(NMI)提供的参比物质进行比对分析而对其进行验证。
6 分析偏差的估计
无论上述分析偏差在被测组分的整个含量范围内是不变的，或者是摩尔分数的函数，都可以通过试验气体的重复分析来确定其分布范围(即测量不确定度)。在线分析仪性能评定过程中，通常以每组重复测量(数据)的响应平均值来确定响应函数，该响应函数可能是一级、二级或三级多项式。多项式级别越高，其应用过程就越复杂。
理论上需要通过测量无限多个、组成位于规定操作范围内的试验气体混合物，才能对仪器引起的误差及其不确定度范围进行完整的评估。但实际工作中通常采用的评估方法原理是：在预定的含量范围内测量少数几个试验气体，并据此确定每个组分响应函数的数学表达式，然后用这些真实响应函数、仪器数据系统的假定响应函数，以及仪器所采用的标准气体混合物(RGM)的具备溯源性的标准值(参考数据)来模拟仪器的性能。最后用迭代方法对气体混合物进行大量的离线模拟测量，从而确定在线分析系统本身固有的性能基准。
目前，工业上通常采用ISO 10723规定的程序，以ISO 6974(或GB/T 13610)规定的分析方法对在线分析仪进行操作性能评价，从而确定其分析偏差的分布范围(不确定度)。按ISO 10723的规定，对于每个组分需要涵盖测量范围的7个不同浓度来定义三级多项式。如果经验表明不可能是三级多项式时，也可以5个浓度来定义二级响应函数，或以3个浓度定义一级响应函数。但对于应用天然气能量计量的组成分析而言，一般均倾向于使用涵盖测量范围的7个浓度。
以下介绍英国EffecTech公司完成的一个在线分析器操作性能评估的实例，评估采用的7个试验气体所覆盖的组成范围是参考英国输气管网对天然气组成的要求而确定的(见表 6)。
表 6
|
表 6 试验气体覆盖的组成范围
|
按照国际标准ISO 6143-2001《气体分析-测定并检查标定用混合气体成分的比较方法》的有关规定，用广义最小二乘法对每个组分已知的摩尔分数及其不确定度进行回归分析，得出在每个摩尔分数(含量条件下)的平均响应值及该响应值的测量不确定度。这样，在不确定度计算中就可使用两种不同的校准函数：响应函数和分析函数。当以仪器响应值(Ri)表示为(组分含量)摩尔分数(xi)的函数时，其数学表达式称为校准函数；而(组分含量)摩尔分数表示为仪器响应值的函数时，其数学表达式则被称为分析函数[2]。
各组分的真实校准函数Fi, true(xi)如式(1)所示：
 |
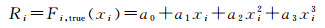(1) |
式中：an为校准函数(多项式)的系数。
真实分析函数Gi, true(Ri)如式(2)所示：
 |
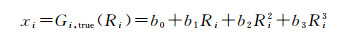(2) |
式中：bn为分析函数(多项式)的系数。
表 7和表 8分别列出了校准函数和分析函数的有关系数。
表 7
|
|
表 7 校准函数的有关系数
|
表 8
|
|
表 8 分析函数的有关系数
|
如果以假定的仪器响应作为分析函数，在线分析仪出厂时默认的设置函数可以式(3)表示：
 |
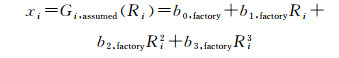(3) |
式中：b1, factory为仪器默认的分析函数(多项式)的系数。
多数情况下，由于默认的设置函数为一条通过原点的直线，因而系数b0factory=b2, factory=b3, factory=0。
用RGM以真实响应函数对假定响应函数进行校准后，测得的未归一化的组分(i)的摩尔分数xi, meas*按(4)式计算：
 |
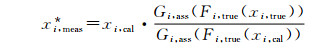(4) |
当按上述程序计算出天然气中所有组分的含量后，可按式(5)进行归一化：
 |
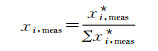(5) |
式中：xi, meas为归一化后的组分(i)的摩尔分数。
按归一化组成计算物理性质Pmeas时(如发热量)，可以由式(6)计算组分分析的误差，由式(7)计算发热量的误差：
 |
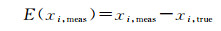(6) |
 |
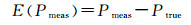(7) |
7 Monte-Carlo模拟
Monte-Carlo模拟的实质是：利用少量实验室试验得到的真实响应函数(包括校准函数和分析函数)，及其与假设响应函数和不同RMG组成之间的关系，通过化学计量学的方法，在大范围内用计算机模拟在线分析仪的操作性能，从而确定(样品气)经归一化的摩尔组成和物理性质的误差分布。具体试验方案为构建一个至少应包括10 000个随机样品气组成的数据集，其中各组分摩尔分数皆位于所考虑的全部计量站可能出现的天然气组成范围内。
严格说来，模拟样品中所采用的组成并不完全是随机的，而是通过某种组分的含量与同类组分中相邻组分含量的(已知)关系获得的。例如，天然气(组成)发生器对有关C4H10、C5H12的异构体与正构体的关系就采用了这些规则。因而采用此方法时，非自然界生成的天然气组分就不会出现于模拟样品之中。同时，在设计模拟组成时也必须考虑国家或地区对商品天然气的有关法律、法规和标准。例如，我国强制性国家标准GB 17820《天然气》规定，商品天然气的高位发热量不能低于31.4 MJ/m3，CO2体积分数不能高于3.0%等。
将每个模拟组成样品测定的有关组分含量及据此计算的发热量的误差制成表格，从而求出每个组分含量及据此计算的发热量的平均误差(见表 9)。
表 9
表 9 商品天然气中典型组分在组成范围内的平均误差
|
表 9 商品天然气中典型组分在组成范围内的平均误差
|
按英国法规的规定，在贸易交接计量点的结算界面上，典型的高位发热量的最大允许偏差(MPB)应不超过0.02 MJ/m3，表 9所示的平均误差远低于此值。
由10 000个不同组成样品模拟计算得到的发热量分析偏差分布如图 4所示，该分布是CH4含量的函数。其它组分也会影响该误差，但CH4作为主要组分，对误差的影响最大；相对于CH4而言，绝大多数情况下其它组分的影响可以忽略。从图 4可以看出，当样品气中甲烷含量接近其在RGM中的含量(80.5%(y))时，误差扩散的区域最小；而样品气中CH4含量越高则误差分布范围越大。
8 不确定度评定
8.1 未归一化组分含量的标准不确定度
天然气气相色谱分析中，组分含量分数误差和据此计算物性误差是由于仪器的真实响应函数和假定响应函数存在差别而产生的；但被测组分含量分数和物性的不确定度则是由RGM的组成和仪器精密度的不确定度产生的。
由于模拟中所采用的假设组分含量的真值yi, actual和由其计算的物理性质Pactual的不确定度为零，因此误差不确定度u(E(x))和u(E(P))分别等于被测组分含量的不确定度u(yi, meas)和计算物性的不确定度u(Pmeas)。
如果仪器经单点校准，或各组分近似地可由仪器系统的某个非理想分析函数来确定时，上述方程(4)可简化为方程(8)：
 |
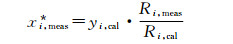(8) |
式中：xi，meas*为被测样品中组分i未归一化的含量；yi，cal为RGM中组分i的含量；Ri，meas为测定样品中组分i时仪器响应值(积分面积或峰高)；Ri，cal为测定RGM中组分i时仪器响应值(积分面积或峰高)。
按式(8)所示，可以通过式(9)求有关项的相对不确定度的平方和即可求得被测组分(i)未归一化含量的标准不确定度。
 |
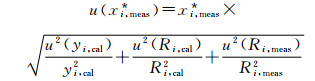(9) |
由式(9)可以看出：被测组分未经归一化的含量分数的标准不确定度由3个来源计算：RGM本身的不确定度、RGM响应函数的不确定度和样品气响应函数的不确定度。
8.2 响应值的标准不确定度
响应值的标准不确定度u(R)可以由在线分析仪操作性能评价所确定的精密函数通过式(10)和式(11)来估计：
 |
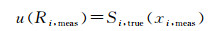(10) |
 |
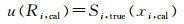(11) |
式中：Si, true(xi)为组分(i)的精密度函数。
响应值的标准偏差(标准不确定度)pi可以表示如下：
 |
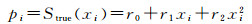(12) |
式中：rn为精密度函数(多项式)的有关系数；pi为仪器对组分i的响应值的标准偏差(标准不确定度)。
利用在线分析仪取得的被测组分含量数据，按国家标准GB/T 11062《天然气发热量、密度、相对密度和沃泊指数的计算方法》的规定计算商品天然气高位发热量时，计算值的不确定度主要来源于以下三个方面：
(1) 天然气中各组分在不同燃烧参比条件下的(理想)发热量数据表中的基础数据可能产生的不确定度。
(2) 使用上述数据的计算方法的偏差。
(3) 作为计算方法输入数据的不确定度。经验表明，按上述方法计算高位发热量时，计算值的不确定度主要来源于被测组分含量分析数据的不确定度，来源于(1)和(2)的不确定度对合成(总)不确定度的贡献很小，可以忽略不计。因此，由被测组分含量的不确定度u(xi,meas)就可以直接估计高位发热量的不确定度u(P)。
8.3 合成不确定度
由于误差是以代数和的方式相结合，而不确定度则是以方和根的方式相结合，故误差与这些误差的不确定度不可能以令人满意的方式相结合，通常只能对两者进行比较。以往商品天然气的组成分析误差超过测量不确定度的点，为限制符合仪器要求的组成范围提供了有用的基准。但目前常见的做法是接受组成的测量误差，只要该误差不会给高位发热量的计算造成不可接受的误差。鉴此，必须对(组成分析的)未校正误差对测量合成(总)不确定度做出评价，并将评价得到的合成不确定度与在线分析仪的性能规格进行对比。
8.3.1 组分含量和发热量的平均误差
组分含量或发热量的平均误差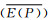
按下式计算：
 |
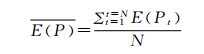(13) |
式中：E(Pt)为计算的N个假设组成(通常为10 000个)中第t个组成的组分含量或发热量的测量误差。
8.3.2 平均误差的合成(标准)不确定度
按以上方法确定的平均误差的合成(标准)不确定度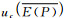
即为通过式(14)求得的正方根：
 |
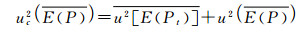(14) |
式中：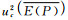
为平均误差的标准不确定度的平方，它是由10 000个假设组成中每个组成的测定误差的方差计算而得；
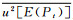为10 000个假设组成中每个组成误差标准不确定度平方的算术平均值，而
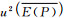则由10 000个假设组成中每个组成的测量误差求得。
8.3.3 平均误差的扩展不确定度和MPE
按我国国家计量技术规范JJF 1059《测量不确定度评定与表示》的规定，扩展确定度(U)等于合成不确定度(uc)和包含因子(k)的乘积；也可以用置信度的区间的半宽来表示。目前，天然气能量计量系统扩展不确定度使用的包含因子k=2，置信度为95%。
如果存在最大允许误差(MPE)的条件，符合式(15)所示的关系式则表明存在MPE的条件；此条件即为“平均误差的绝对值加上平均误差的合成不确定度不大于最大允许误差(MPE)”。
 |
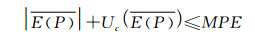(15) |
8.4 发热量与MPB及MPE的关系
按Monte-Carlo模拟结果得到的发热量数据与MPB的关系如图 5所示。图 5中的高斯曲线表示模拟过程中单个测量误差(数据)的分布，当商品天然气中CH4摩尔分数在78%~98%范围内变化时该曲线面积的绝大部分落在MPB带内。图 6利用与图 5相同的数据绘制，但按式(15)所示考虑了平均误差的不确定度。图 6所示数据同样表明当商品天然气中CH4摩尔分数在78%~98%范围内变化时该曲线面积的绝大部分落在MPE带内。因此，图 6所示数据表明能量计量系统测量商品天然气高位发热量的分析偏差及其不确定度均符合有关法规和标准的要求。
9 结论
(1) 天然气能量计量系统的分析偏差的分布范围即为其不确定度。
(2) 在利用RGM溯源的过程中，并非对单个分析数据进行验证，而是在特定的组成范围内以规定的分析程序，对大量不同组成的样品气进行验证。
(3) 为保证验证结果的可靠性，应采用化学计量学的方法进行取样模拟和实验设计，应建立一个至少包括10 000个随机样品气组成的数据集进行验证。
(4) Monte-Carlo模拟(验证)结果表明，由英国管网输送的商品天然气，当其中CH4摩尔分数在78%~98%范围内变化时，商品天然气高位发热量测量的分析偏差及其不确定度均符合有关法规和标准的要求。
| [1] |
黄黎明, 陈赓良, 张富元, 等. 天然气能量计量的理论与实践[M]. 北京: 石油工业出版社, 2010: 7.
|
| [2] |
罗勤, 陈赓良. 天然气国家标准实施指南[M]. 北京: 中国标准出版社, 2006: 8.
|
| [3] |
常宏岗, 罗勤, 陈赓良. 天然气气质管理与能量计量[M]. 北京: 石油工业出版社, 2008: 3.
|
| [4] |
Southwest Research Institute. Development and Evaluation of a Gas Chromatograph Test Protocol[R], SwRI Project No.18.13576, 2008.
|
| [5] |
|
2012, Vol. 41