石油与天然气化工  2012, Vol. 41 Issue (5): 533-536
天然气管道投产氮气置换混气规律研究
赵孟卿1 , 李灿荣1 , 陈川2 , 谢尧3 , 周精田4 , 胡学兵1 , 高杨1     
1. 中国石油集团东南亚管道有限公司;
2. 吐哈油田三塘湖采油厂;
3. 中海油海洋石油工程股份有限公司;
4. 中国石油西南油气田公司输气管理处
收稿日期：2011-12-27；修回日期：2012-04-02
作者简介：赵孟卿(1987-)男，硕士，2011年毕业于西南石油大学油气储运工程专业，现在东南亚管道公司工作。地址：(100028)北京市朝阳区太阳宫金星园8号A座。E-mail：zhaomengqing@126.com.
摘要：天然气管道投产过程中有许多置换方法，其中常采用的是无隔离器氮气置换。目前，对于氮气置换混气规律的研究还处于发展阶段。以一维对流扩散方程为基础讨论了氮气置换模型中3种范宁摩擦系数对混气规律的影响，分析了一维模型中各种范宁摩擦系数适用的条件，同时对氮气置换过程的二维混气模型进行了初步论述，并对两种模型的适用条件进行了比较。
关键词：氮气置换    一维模型    范宁摩擦系数    二维模型    
Research on the nitrogen replacement aerating law during the natural gas pipeline commissioning
Zhao Mongqing1 , Li Canrong1 , Chen Chuan2 , et al     
1. Southeast Asia Pipeline Company, CNPC, Beijing 100028, China;
2. Santanghu Oil Production Plant in Tuha Oilfield, Hami 839009, Xinjiang, China
Abstract: There are many replacement methods in the process of natural gas pipelines commissioning, and the commonly most used one is nitrogen replacement without isolator. The current research on the aerating law of nitrogen replacement is still in development stage. Based on one-dimensional convection-diffusion equation, this paper discusses the influence of three kinds of Fanning friction factors on the aerating law in the nitrogen replacement, analyzes the application conditions of the Fanning friction factors in one-dimensional model, discusses preliminarily the two-dimensional aerating model in nitrogen replacement, and compares the two kinds of models application conditions.
Key words: nitrogen replacement    one-dimensional model    Fanning friction factor    two-dimensional model    

天然气置换过程是天然气管道投产的关键技术，其技术难点在于安全、高效、科学、经济地将管道内的天然气与空气进行隔离，以防止形成爆炸性混合物。虽然，近几年国内天然气管道相继建成投产，但是对置换工艺技术尚没有进行系统的研究，相关技术规范也没有提出明确的要求。国外文献资料中也缺乏置换工艺技术相关的研究成果，因此对置换过程中混气规律的研究显得越发重要[1]。科学认识混气过程，合理确定混气模型在天然气置换过程中起着举足轻重的作用。

1 常用置换方案

天然气管道投产过程中常用的置换方法有加隔离器氮气隔离置换、不加隔离器氮气隔离置换和加隔离器无氮气置换3种[2-4]。清管器在管内运行阻力在不断地变化，因此清管器运行速度难以得到控制。结合国内西一线、涩宁兰等输气管道投产经验，可知加清管器置换并未达到隔离气体、减少混气量的目的。根据实践经验对这3种输气管道置换方案应用效果进行对比总结，各种方案的优缺点如表 1所示。

表 1    常用置换方案比较表

2 一维氮气置换模型

天然气管道在置换过程中，由于两种气体存在着速度梯度和浓度梯度，在分子扩散和对流扩散的作用下(主要是对流作用)，在接触界面会发生质量传递，即混气，如图 1所示。

图 1     混气过程示意图 (O混气初始接触面；X-计算点距离初始接触面的距离，m; L-混气发生段的长度，m; kA, kB-对流扩散系数, m2/s )

由于天然气管道的直径和长度相比可以忽略不计，所以可以假设天然气沿径向分布均匀，并且不存在径向浓度梯度。将空气视为单一物质，用一维对流扩散方程描述管内断面混气平均浓度分布，其方

程和边界条件见式(1)[5]。

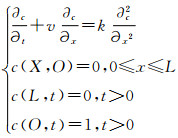(1)

式中：c为组分的摩尔浓度，mol/m3；v为流体速度，m/s；t为时间，s；k为对流扩散系数，m2/s；其余符号意义见图 1说明。

式(1)求解的核心是对流扩散系数的确定。当管道流体处于层流状态下时，常采用Taylor层流扩散系数[6]，见式(2)。

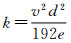(2)

式中:k为层流扩散系数，m2/s；v为平均流速，m/s；e为分子扩散系数，m2/s；d为管道直径，m。

然而，在天然气输送过程中天然气常处于紊流状态下，Taylor层流扩散系数此时不再适用。由于湍流扩散机理比较复杂，目前还没有一个通用的对流扩散系数求解公式。本文引用3个对流扩散系数的计算公式。当天然气雷诺数(Re)大于2×104时可采用Taylor对流扩散系数计算公式[7]，见式(3)。

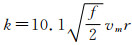(3)

式中：k为对流扩散系数，m2/s；f为范宁摩擦系数；vm为圆管截面的主体平均速度，m/s；r为管道半径，m。

式(3)中范宁摩擦系数的选取不同，得到的湍流扩散系数也会有变化。常用的有Goldstein公式(见式(4))和Colebrook-White公式(见式(5))。

(4)
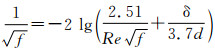(5)

式中：δ为管道绝对当量粗糙度，m；d为管道直径，m；f为范宁摩擦系数。

式(4)适用的范围为3×104≤Re≤106。在摩擦系数计算公式中，Colebrook-White公式最为精确，式中f为隐函数，求解时需采用编程计算。程序运行界面如图 2所示(式(5)和式(3)，C++Builder6.0)。

图 2     程序运行界面图

美国天然气研究院(GRI)经过长期对管道内气体置换的研究发现，扩散系数不仅与管径、置换流速与Re有关，还与施密特数(Sc)有关，如图 3所示。

图 3     湍流扩散系数与置换流速、管径和施密特数关系图

由于空气、氮气和甲烷的Sc约为1.0，图 3中Sc=1.0时的曲线可以通过式(6)来描述[8]。

(6)

式中：k为对流扩散系数，m2/s；μ为天然气运动粘度，m2/s；d为管径，m；Re为雷诺数。

当管线上存在弯头时，湍流扩散的作用会增加，引用Bischoff公式分析管线弯头对湍流扩散的影响，见式(7)。

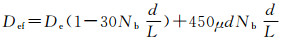(7)

式中：Def为考虑弯头的湍流扩散系数，m2/s；De为直管路中不考虑弯头影响的扩散系数，m2/s；Nb为弯头个数; d为管道直径，m；L为管道长度，m; μ为天然气运动粘度，m2/s。

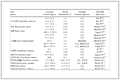
为了研究3种范宁摩擦系数的适用性，GRI曾对8条采用“无隔离器气推气”置换方式的天然气管线进行了观测[9]。其结果如表 2所示：

表 2    3种范宁摩擦系数对比表

由表 2可知3种对流扩散系数随着管径和置换速度的增大而增大，然而置换过程中天然气置换速率不能太小，避免天然气处于层流状态以减少混气长度；扩散系数从小到大排列为GRI、Taylor和Taylor-CW。对于弯头少的长距离输气管道一般可忽略弯头对扩散系数的影响。通过对输气管道置换实测，建议Taylor-Cw计算公式应用于短距离、小管径或者流速很低的置换过程，GRI计算方法应用于长距离、大管径、高流速的置换过程。

3 二维氮气置换模型

由于天然气管道在投产过程中管内流场和速度场在周向没有变化，并且气体常在紊流状态下流动，因此置换过程可用二维紊流扩散模型来建立动力学模型。二维氮气置换模型常用FLUENT软件对其规律进行仿真模拟，应用非稳态数值模拟方法，采用化学模型中的“组分传输模型”，并应用EXCEL将FLUENT导出的数据进行图像化处理，可以直观地看出各个变量发展和变化的趋势，从而得出天然气管道投产中的混气规律。

当采用FLUENT软件模拟时，以氮气进入管线的进口设为速度入口，管线的出口设为压力出口，管线管壁设为固体壁面，用绝对压力减去操作压力，得到计量压力，采用结构化四边形方法划分网格，壁面处网格加密可进行迭代计算。

氮气、空气沿管壁湍流流动时，其内部存在3个不同的区域，它们依照距离管壁的次序分别是层流内层、缓冲层和湍流核心。在层流内层，Ds=Dm；缓冲层，Ds=Dm+εM；湍流核心，Ds=εM。其中，Dm为分子扩散系数；Ds为某组分的扩散系数；εM为湍流扩散系数[10]。管内紊流动能方程k和扩散方程ε分别见式(8)与式(9)。

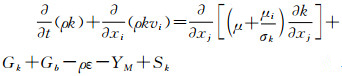(8)
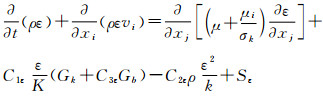(9)

式中：ρ为组分的浓度；ε为耗散率；μi为i组分的动力粘度；vi为i组分的时均速度；Gk为代表由层流速度梯度而产生的紊流动能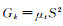，；S为应力张量系数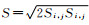，；Gb为代表浮力产生的紊流动能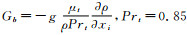，；YM为可压缩紊流流动中所有扩散速度的扩散损耗；Si, j为时均应变率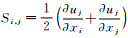，；C1ε、C2ε、C3ε为经验常数。

σk和σε是与湍流动能k和耗散率ε对应的湍流Prandtl数，Sk和Sε是用户定义的源项。根据Launder等的推荐值及后来的实验验证，模型常数C1ε、C2ε、C3ε、σk、σε的取值为：C1ε=1.44，C2ε=1.92，C3ε=0.09，σk=1.0，σε=1.3。

密度ρ采用理想气体计算公式，见式(10)。

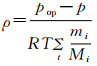(10)

式中：p为局部相对压力，Pa；pop为操作压力(本模拟中设为大气压)，Pa；R为通用气体常数，8.314 J/(mol·K)；mi为第i种物质的摩尔浓度，mol/L；Mi为第i种物质的分子量；T为混气温度，℃。

粘度μ使用分子运动论定义流体的粘度，见式(11)。

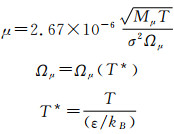(11)

式中：T为混气温度，℃；Mμ为第μ种物质的分子量; σ为能量参数，埃(10-10m)；ε/kB为特征长度。ε/kB与σ是该种流体的分子运动论参数，即Lennard-Jones参数。

4 结论与建议

虽然一维氮气置换模型能反应气体的基本混气规律，但是无法得出具体的混气过程，以及管道流体在运行过程中混气段的形成、发展以至具体浓度分布等细节信息与规律。一维置换模型对对流扩散系数的依赖性很强，然而对流扩散系数须经现场经验或实验测定，具有很大的不确定性。置换模型的二维动力学模型则不存在上述问题，对流扩散系数对二维模型的影响较小，然而正确建立置换模型是二维置换模型合理与否的关键因素。

参考文献
[1]
许玉磊. 输气管道"气推气"投产过程混气规律研究[J]. 油气储运, 2008, 27(1): 11-12.
[2]
刘雪梅, 谢英. 输气管道气体置换方案的比较及应用[J]. 油气储运, 2008, 27(1): 47-50.
[3]
邓晓峰, 何永春, 彭维茂, 等. 天然气管道氮气干燥置换工艺及实际应用[J]. 石油与天然气化工, 2011, 40(3): 325-328. DOI:10.3969/j.issn.1007-3426.2011.03.026
[4]
薛继军, 张鹏云, 王俊奇, 等. 输气管道投产置换过程气体混合规律研究[J]. 天然气工业, 2006, 26(12): 147-149. DOI:10.3321/j.issn:1000-0976.2006.12.042
[5]
付春丽.海管氮气置换混气规律研究[D].北京: 中国石油大学, 2009: 11-22. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1551658
[6]
Taylor G I. Dispersion of soluble matter in solvent flowing slowly through a tube[J]. Proc.Roy.Soc.A, 1953, 219(1137): 186-203.
[7]
Taylor G I. The dispersion of matter in turbulent flow through a pipe[J]. Proc.Roy.Soc.A, 1954(223): 446-468.
[8]
Ekambara K, Joshi J B. Axial mixing in laminar pipe flows[J]. Chemical Engineering Science, 2004(59): 3929-3944.
[9]
Johnson J E. Pipeline Purging Principles and Practice[J]. Journal of Offshore Mechanics and Arctic Enginnering, 1998, 2(10): 249-256.
[10]
李万平. 计算流体力学[M]. 武汉: 华中科技大学出版社, 2004: 121-127.
X